公务员考试行测概率问题中常见的考点有古典型概率、独立事件、重复试验、多次独立重复试验、几何概率、期望、分层抽样、条件概率等。由于概率问题涉及的考点多、散等原因，许多考生在看到这一类题目是便选择了望而却步。而其实在公务员考试中，由于考试时间所限，解答概率问题必须加快运算速度。接下来安徽公务员考试网 (www.anhuigwy.org）将对此类问题中的一个典型考点多次独立重复试验进行详细梳理，助公考成功。

 

　　一、什么是伯努力试验

　　在同样条件下重复地、各次之间相互独立的进行的一种试验。

　　二、题型特征

　　在这种试验中，每一次试验只会有两种结果，即A事件要么发生要么不发生，并且每次发生的概率都是相同的。

　　三、判断方法

　　判断是否为伯努力试验的关键是每次试验事件A的概率不变，并且每次试验的结果同其他各次试验的结果无关，重复指的是试验为一系列的试验，并非一次实验，但要注意重复事件发生的概率相互之间有没有影响。

　　四、计算公式

　　某一实验独立重复n次，其中每次试验中某一事件A发生的概率是p，那么事件A出现k次的概率为：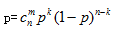

　　五、常见题型

　　例1：天气预报正确的概率为0.8，则3天的天气预报恰有两天正确的概率为多少?

　　【解析】符合独立重复试验的条件，可直接套用公式，求出结果P= 0.384。

　　例2：某乒乓球男子单打决赛在甲乙两选手间进行，比赛采用7局4胜制。已知每局比赛甲选手战胜乙选手的概率均为0.7，则甲选手以4：1战胜乙选手的概率为多少?

　　【解析】这道题目很多考生会直接套用多次独立重复试验，孰不知正好踏入了命题老师设置的陷阱，因为甲选手需要4:1战胜乙选手，这就要求最后一局一定是甲选手胜，前面的四场比赛中甲恰好胜三场，因此这道题目分为两个阶段，第一阶段甲在四次中胜三次，第二阶段甲胜，第一阶段才为独立重复试验。所以。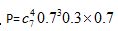

 

　　更多解题思路和解题技巧，可参看2017年公务员考试技巧手册。