在公务员考试行测数学运算中，有一类植树问题，这类题目没有什么解题技巧，而是利用对应的公式就可以很容易的解答，那么，接下来安徽公务员考试网就帮考生总结一下植树问题所用到的公式以及怎么应用。

　　一、植树问题的类型和应对公式

　　例如：在一周长为100米的湖边种树，如果每隔5米种一棵，共要种多少棵树？这样在一条“路”上等距离植树就是植树问题。在植树问题中，“路”被分为等距离的几段，段数=总路长÷间距、总路长=间距×段数。

　　根据植树路线的不同以及路的两端是否植树，段数与植树的棵数的关系式也不同，下面就从不封闭路线的植树和封闭路线植树来一一说明。

　　（1）不封闭植树：指在不封闭的直线或曲线上植树，根据端点是否植树，还可细分为以下三种情况：

　　①两端都植树：两个端点都植树，树有6棵，段数为5段，即有植树的棵数=段数+1，结合段数=总路长÷间距，则：棵数=总路长÷间距+1，总路长=（棵数-1）×间距。

　　②两端都不植树：两个端点都不植树，可知植树的棵数=段数-1，结合段数=总路长÷间距，则：棵数=总路长÷间距-1，总路长=（棵树+1）×间距。

　　③只有一端植树：只有一个端点植树，可知植树的棵数=段数，结合段数=总路长÷间距，则：棵数=总路长÷间距，总路长=棵数×间距。

　　（2）封闭植树：指在圆、正方形、长方形、闭合曲线等上面植树，因为头尾两端重合在一起，所以种树的棵数等于分成的段数。所以棵数=总路长÷间距，总路长=棵数×间距。

　　二、两边植树问题

　　除了在路的一边植树外，还有路的两边都植树的情况，这时就要先判断出植树类型，计算出一边植树的情况，再根据一边求两边情况。

　　【例题1】如果每500米远架一根电线杆，则30公里需要架设多少根电线杆？

　　A.31 B.30 C.61 D.60

　　解析：此题答案为C。共需要架设30×1000÷500+1=61根电线杆。

　　三、不同间隔植树问题

　　在一些植树问题中，往往存在两种或多种植树方式。这种情况下，就会出现重复植树问题，常需要结合最小公倍数找出重合点。

　　【例题2】某工地从一条直道的一端到另一端每隔3米打一个木桩，一共打了49个木桩。现在要改成4米打一个木桩，那么可以不拔出的木桩共有多少个？

　　A.8 B.9 C.11 D.13

　　解析：此题答案为D。每隔3米打一木桩对应每隔3米植树，两端都打对应两端都植树，因此直道的总长=段数×间距=（棵数-1）×间距=（49-1）×3=144米。

　　依题意，不拔出来的木桩距离起点的距离必须能被3和4整除，3和4的最小公倍数是12，即从起点开始每隔12米有一个木桩可以不拔出，144÷12=12，故有12+1=13根木桩不用拔出。

　　四、植树问题变形

　　在数学运算中还有一些变形题，如锯木头、走楼梯等实际问题，这些变形只是形式上的改变，其本质仍然是植树问题。中公教育专家发现，在最近几年的行测考试中，植树问题往往以这种变形题出现。

　　解决植树问题的变形题，要注意端点是否“植树”，分清“棵数”与“段数”之间是+1还是-1。

　　常见的变形题：锯木头、爬楼梯、重合、队列问题均可视为两端都不植树问题，其中的知识要点如下：

　　锯木头：要锯成n段，则需锯（n-1）次；

　　爬楼梯：从1层到n层，需爬（n-1）段楼梯；若每爬完一段，休息一次，则需休息（n-2）次；

　　重合问题：n段接在一起，重合的有n-1段；

　　队列问题：有n个人（或n辆车），中间有n-1个空。

　　【例题3】把一根钢管锯成小段，一共花了28分钟。已知每锯开一段需要4分钟，这根钢管被锯成了多少段？

　　A.3 B.4 C.6 D.8

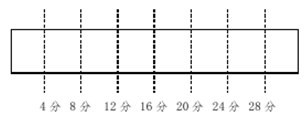
　　解析：此题答案为D。要求钢管被锯的段数，必须首先求出钢管被锯开几处。

　　从上图我们可以看出钢管有28÷4=7处被锯开，因而锯开的段数有7+1=8段。题中被锯开的地方即植树位置，因此问题相当于“两端都不植树”问题，棵数=段数-1。

　　上面几道例题基本套用公式，分清楚类型就可以迅速作答了。希望可以帮助考生把植树问题的解题思路理清，以后再碰到这类问题就不会再花费大量的时间了。

      行测更多解题思路和解题技巧，可参看2015年公务员考试技巧手册。