今天给大家带来的是行测数学运算解题技巧梳理的第五期，也是最后一期了。本期主要介绍如何利用数字特性法排除无关的选项，甚至能帮我们直接选出答案的。详情如下：
看过了解题方法，我们还是先通过一道真题来看一下——
【经典真题】
两箱同样多的蛋黄派分别分发给两队志愿者做早餐，分给甲队每人6块缺8块，分给乙队每人7块剩6块，已知甲队比乙队多6人，则一箱蛋黄派有（）块。
A.120 B.160 C.180 D.240
【解析】正确答案为B。此题很简单，只要利用数字特性法能直接帮我们排除不正确的选项，具体如何操作呢，来看老师分析。
以上视频截取自国考系统班，更多视频解析查看链接：http://www.chinaexam.org/course/list?tag=2。
听完了老师讲解，是不是觉得茅塞顿开了呢，大家一鼓作气，再通过3道真题来练练手吧。
【例1】（2018年国考省级以上试卷第75题）一辆汽车第一天行驶了5个小时，第二天行驶了600公里，第三天比第一天少行驶200公里，三天共行驶了18个小时。已知第一天的平均速度与三天全程的平均速度相同，则三天共行驶了多少公里（）。
A．800 B．900 C．1000 D．1100
【解析】正确答案为B。
本题利用数字特性法，因全程的时间为 18 小时，故路程应为 18 的倍数，四个选项中只有 900 符合。因此 B 项当选。
【例2】（2017年国考副省级级试卷第62题）某人出生于20世纪70年代，某年他发现从当年起连续10年自己的年龄与当年年份数字之和相等（出生当年算0岁）。问他在以下哪一年时，年龄为9的整数倍（）。
A．2006年 B．2007年 C．2008年 D．2009年
【解析】正确答案为B。
方法一：设出生年份为1970+x年。若当年为1980+A年，根据连续10年自己的年龄均与当年年份数字之和相等，可得：(1980+A)-(1970+x)=1+9+8+A，解得x=-8，不满足条件；若当年为1990+B年，可得：(1990+B)-(1970+x)=1+9+9+B，解得x=1，即出生于1971年，依次代入选项：2006年为35岁，不符合9的整数倍，排除A；2007年为36岁，是9的整数倍，符合题意。故正确答案为B。
方法二：若1980年，数字之和为1+9+8+0=18，若满足年龄等于当年年份数字之和，则出生年份=1980-18=1962，不满足出生于20世纪70年代；若1990年，数字之和为1+9+9+0=19岁，若满足年龄等于当年年份数字之和，则出生年份=1990-19=1971，满足出生于20世纪70年代，且从1990年开始连续十年都满足要求。所以出生年份为1971年，依次代入选项2006年为35岁，不符合9的整数倍，排除A；2007年为36岁，是9的整数倍。符合题意。
【例3】（2018年浙江A类第64题）小王购买甲、乙两种特价商品。甲商品打八折后每件52元，乙商品打八五折后每件34元，小王购买这些商品总共比打折前节省了83元。问他购买这两种特价商品总共支出了多少元？
A.544 B.445 C.427 D.362
【解析】正确答案为D。
根据甲商品打八折后每件52元，可计算出甲的售价为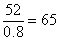
元；根据乙商品打八五折后每件34元，可计算出乙的售价为
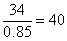元。甲商品一件节省65-52=13元，乙商品一件节省40-34=6元。设购买甲商品x件，乙商品y件，由于小王购买这些商品比打折前节省了83元，可得13x+6y=83，该式为不定方程，结合奇偶特性，可得x=5，y=3，即甲、乙两种商品分别买了5件、3件。购买这两种特价商品总支出为：52×5+34×3=362元。
以上是行测数学运算解题技巧梳理第五期内容，至此数学运算解题技巧已梳理完结。下周开始我们会有全新的内容，敬请期待。
往期阅读：
