10月30日更新的2020年安徽公务员考试每日一练是数量关系题，多做公务员考试模拟题练习不仅有利于掌握考点，而且能够帮助保持题感，潜移默化中熟悉命题。

　　1．现要在一边长为4m的正六边形广场铺设道板砖，每块道板砖均为直角三角形，规格为2m×m×1m，则至少需要多少块道板砖（不考虑道板砖之间的搭接面积）（  ）

　　A．24

　　B．32

　　C．48

　　D．64

　　2．甲、乙两人在圆形小路上同时开始锻炼身体，某日甲跑完5圈时，乙正好散步走完2圈；次日乙走完半圈时，甲才开始跑步（两人均顺时针），乙走完2圈时，甲、乙位于同一位置，距离甲跑步起点25米。问两人次日出发地相隔多少米（  ）

　　A．25

　　B．50

　　C．75

　　D．100

　　3．下表是某地区居民生活用水阶梯价格构成表：

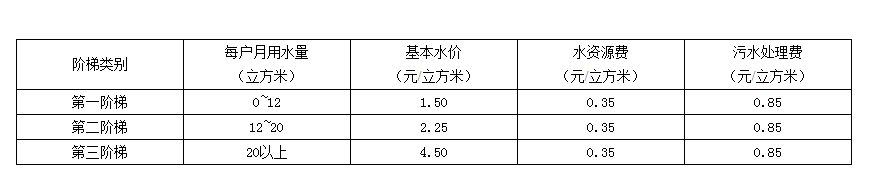
　　已知该地区的小王一家一季度用水共花费180元，问小王一家一季度最多用水多少立方米（  ）

　　A．52

　　B．60

　　C．66

　　D．76

　　4．甲、乙二人玩掷骰子游戏，每次掷一个骰子，甲先掷乙再掷，结果甲两次掷出的骰子数字之和为6，则甲两次掷出的骰子数字分别比乙两次都大的概率是多少（  ）

　　A．5/72

　　B．1/10

　　C．4/54

　　D．1/18

　　5．实验室的小高和小冷都计划将相同的200克的酒精溶液稀释到50%的浓度，但都因为疏忽，小高加了比计划多一半的水，小冷少加了50克水。二人发现，若把二人现在稀释后的酒精溶液混合后也可得到他们想要的50%浓度的酒精溶液。则原来的酒精溶液浓度为（  ）

　　A．75%

　　B．80%

　　C．85%

　　D．90%

　　【下面是参考答案与解析。如果你认为题目或解析有误，可点这里给我们纠错。】

　　1．【解析】C。如下图所示，正六边形可拆分为4个直角三角形和1个长方形，因正六边形内角为120°，则∠BAC=30°，30°对应的直角边为斜边的一半，则BC=2m，根据勾股定理，AC=2√3m，AF=2AC=4√3m。

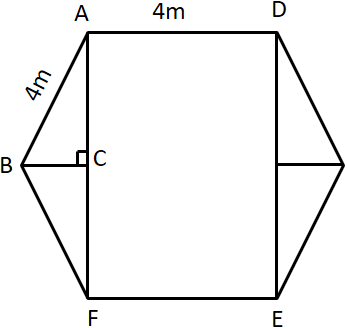
　　直角三角形道板砖，因其与△ABC相似，斜边为AB的一半，√3m的直角边长度为AC的一半，因此△ABC至少需要4块道板砖铺设。

　　两个三角形道板砖可组合成长为√3m、宽为1m的长方形，其长为AF的1/4，宽为AD的1/4，则长方形ADEF需要2×4×4=32（块）道板砖。

　　因此铺设正六边形广场至少需要道板砖4×4+32=48（块）。C项当选。

　　2．【解析】A。行程问题中，时间相同，路程与速度成正比，甲跑5圈与乙走2圈时间相同，则甲、乙速度之比为5:2。次日乙走完剩余1.5圈时，甲跑的圈数为x，x∶1.5=5∶2，解得x=3.75（圈），甲距离跑步起点0.25圈，为25米。此时，乙正好走完2圈，回到散步起点，则两人次日出发地相隔25米。因此A项当选。

　　3．【解析】B。根据题意可知，要使用水最多，则要让单价尽量低，因此先用低价的水，则每月用水量需尽量平均。若每月用水12立方米，则一季度三个月需花水费12×3×（1.50+0.35+0.85）=97.2（元），此时剩余水费为180-97.2=82.8（元）。继续用水则单价将变为第二阶梯水价2.25+0.35+0.85=3.45（元/立方米），82.8÷3.45=24（立方米），则剩余水费恰好可全部购买一季度三个月第二阶梯的水24立方米。所以小王一家一季度用水最多3×12+24=60（立方米）。B项当选。

　　4．【解析】D。根据题意，将甲两次掷出的骰子数字分别比乙两次都大的可能情况分类讨论如下：

　　①甲两次掷出的数字依次为2、4，则两次分别都比乙掷出的数字大的情况有3（种）；

　　②甲两次掷出的数字依次为3、3，则两次分别都比乙掷出的数字大的情况有4（种）；

　　③甲两次掷出的数字依次为4、2，则两次分别都比乙掷出的数字大的情况有3（种）。

　　所以满足条件的情况数共3+4+3=10（种）。而甲掷骰子的总情况有1+5、2+4、3+3、4+2和5+1这五种，乙掷骰子的总情况有（种），所以总情况有5×36=180（种）。因此，甲两次都分别比乙掷出的骰子数字大的概率是1/18。因此D项当选。

　　5．【解析】A。假设计划加入y克水，实际小高加了1.5y克水，小冷加了（y-50）克水。则200克原酒精溶液与y克水可混合为50%浓度的酒精溶液，现在把两人得到的溶液进行混合，相当于400克原酒精溶液与（2.5y-50）克水混合也可得到50%浓度的酒精溶液。则2.5y-50=2y，解得y=100克。即200克原酒精溶液与100克水混合，可得到300克浓度为50%的酒精溶液，溶质质量为300×50%=150（克），故原来酒精溶液浓度为150/200×100%=75%。因此A项当选。